[Coda]

Let's consider p(x) = x² + 1. We know there are two roots, but none of them are real. But what about imaginary roots, now that we know about them?

Well, let's pull out our old friend the quadratic formula. a=1, b=0, c=1, so:

x = (-0 +/- sqrt(0² - 4*1*1))/(2*1)
x = +/- sqrt(-4) / 2
x = +/- 2sqrt(-1) / 2
x = +/- sqrt(-1)
x = +/- i

So x = i and x = -i are the imaginary roots of the function!



Now, if you want to think about what complex numbers LOOK like... It gets complicated!

If real numbers are one-dimensional, then complex numbers are two-dimensional. If functions of real numbers can be plotted in two dimensions... functions of complex numbers are plotted in FOUR. That's not easy to imagine on its own!

But you CAN think of it as a FIELD.

Imagine the real number line. If you were to map a function over it, then each point on that line would have a corresponding number for the value of the function at that point.

For complex numbers, imagine a plane. If you consider f(x + yi) -- that is, the real part of the number along the x axis, and the imaginary part along the y axis -- then you can evaluate the function at any point on the plane, and the result is a two-dimensional vector. For example, this is a graph of the function f(x) = (x + 2)(x - 2), if you allow x to take on complex values:



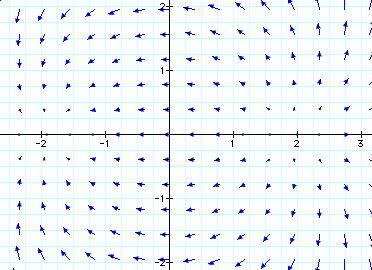
With a graph like this, the roots are the places where the length of the vector is zero. The real roots are places where this is true on the x axis. The imaginary roots are places where this is true on the y axis. There could also be complex roots: Consider the function f(x) = x⁴ + 1. We know it has to have four roots, but we can obviously see that none of them are real... Let's solve it anyway!

(Lots of algebra, put in a spoiler for brevity)

First off, let's try to factor x⁴ + 1 some.

Let's say y = x², so we can rewrite this as y² + 1. And we already figured out the roots of that one up above, so we know that this factors out to (y - i)(y + i), which is (x² - i)(x² + i).

Now we have to factor each of those factors... One of those is a=1 b=0 c=-i and the other is a=1 b=0 c=i. The quadratic equation comes into play again: (Going ahead and taking out the b terms)

a=1 b=0 c=i
x = +/-(sqrt(-4*1*i))/(2*1) = +/-sqrt(-4i)/2 = +/-2sqrt(-i)/2 = +/-sqrt(-i)

a=1 b=0 c=-i
x = +/-(sqrt(-4*1*-i))/(2*1) = +/-sqrt(4i)/2 = +/-2sqrt(i)/2 = +/-sqrt(i)

So... what's sqrt(i)? Well... Complex numbers are of the form (a+bi), and we know that sqrt(i) * sqrt(i) = i by the definition of square roots, so we put these two things together to say:

sqrt(i) = a + bi
i = (a + bi)²
i = a² + 2abi + (bi)²
i = a² + 2abi - b²
0 + i = (a² - b²) + 2abi

Oh wait a sec. We've got a real number plus an imaginary number on both sides there! And since you can't turn a real number into an imaginary number via addition (you already know that you always get a real number when you add two real numbers) then that means that we can break that up:

0 = a² - b²
--and--
i = 2abi

i/(2ai) = b
1/(2a) = b

0 = a² - (1/(2a))²
0 = a² - 1/(4a²)
0 = a² - 1/(4a²)
--multiply by 4a²--
0 = 4a⁴ - 1
--factor using (x² - 1) = (x + 1)(x - 1)--
0 = (2a² + 1)(2a² - 1)

Since each of these factors must each equal zero, let's consider the second one, since we know the first one is going to end up with an imaginary root again and that's just going to run us all the way back to the top.

0 = 2a² - 1
1 = 2a²
1/2 = a²
sqrt(1/2) = a

Oh hey, that looks useful!

1/(2a) = b (from earlier)
1/(2sqrt(1/2)) = b
1/sqrt(4/2) = b
1/sqrt(2) = b
1/2 = b²
sqrt(1/2) = b

So that means sqrt(i) = sqrt(1/2) + sqrt(1/2)i!

Plugging our answer back into our earlier result of +/-sqrt(+/-i)... Well, that means we need sqrt(-i), but that's sqrt(-1 * i) = sqrt(i)*i = sqrt(1/2)*i + sqrt(1/2)*i*i = sqrt(1/2)*i + -sqrt(1/2).

Therefore, the four complex roots of f(x) = x⁴ + 1 are +/-sqrt(1/2) +/- sqrt(1/2)i. No real roots! No imaginary roots! But if you take (x - sqrt(1/2) - sqrt(1/2)i)(x - sqrt(1/2) + sqrt(1/2)i)(x + sqrt(1/2) - sqrt(1/2)i)(x + sqrt(1/2) + sqrt(1/2)i) and multiply it out, sure enough you get back to x⁴ + 1 like we wanted!